Tags:    c#

Introduktion

I denne artikel skal vi kigge på hvordan vi kan implementere Fourier transformationen i C#.

Denne artikel er den anden i en række af artikler om numerisk og/eller finansiel programmering i C#.

Denne artikel omhandler Fourier transformationen som er en metode vi kan bruge til at finde ud af hvilke frekvenser der udgør et signal. Typiske signaler er lyd og billeder, og Fourier transformationen er et værktøj der hyppigt bruges indenfor feltet signalbehandling.

I artiklen skal vi igennem følgende:

• Hvad er en Fourier transformation?


• Den diskrete Fourier transformation i C#


• Brug af Fourier transformationen


• FFT: Fast Fourier Transformation

Jeg har brugt følgende reference under udarbejdelsen af denne artikel: Digital Signal Processing (4th Edition) af John G. Proakis og Dimitris K Manolakis samt Java Number Cruncher: The Java Programmer's Guide to Numerical Computing af Ronald Mak og Technical Java: Applications for Science and Engineering, af Grant Palmer

Hvad er en Fourier transformation?

Indenfor naturvidenskaben og ingeniørvidenskaben arbejder vi tit med signaler af en eller anden form. Disse signaler kan være billeder, lyd o.a. Når vi skal analysere sådanne signaler behandler vi dem ofte i tidsdomænet, hvilket mange gange er den "naturlige" repræsentation af et signal. Tag for eksempel et lydsignal. Normalt når vi snakker om lydsignaler snakker vi om et signal vi kan skitsere på en tid/amplitude graf.

Det er eksemplificeret på følgende graf:



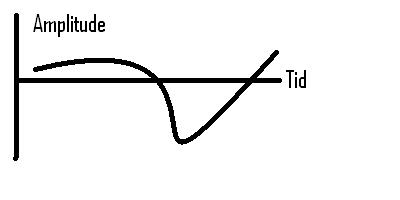
Grafen viser et lydsignal. Den horisontale akse angiver tiden og den vertikale akse signalets amplitude. Så et signals repræsentation i tidsdomænet er den måde hvorpå vi som mennesker oftest opfatter og forstår et signal. I tidsdomænet er et signals amplitude en funktion af tiden:

x = x(t)

Et signal er dog ikke kun karakteriseret ved tid og amplitude, men også ved dets frekvens. Når et signal skal analyseres kan det derfor tit være nyttigt at få viden om hvilke frekvenser der udgør et signal. Denne viden får vi ved at gå fra at arbejde med et signal i tidsdomænet over til at arbejde med det i frekvensdomænet. Og det er netop hvad en Fourier transformation gør for os:



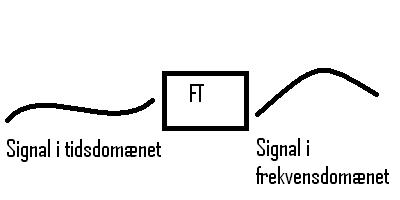
Fourier transformationen gør det muligt at skifte mellem de to domæner. Og bemærk at der er tale om en transformation så absolut intet information går tabt ved at skifte mellem tids og frekvensdomænet med en Fourier transformation. Når vi går fra tids- til frekvensdomænet bruger vi det der hedder en forward Fourier transformation, og når vi skal den anden vej bruger vi den inverse Fourier transformation.

Når vi arbejder i frekvensdomænet er signalets frekvensamplitude en funktion af frekvensen:

X = X(f)
f angiver frekvensen og har enheden Hz ( = 1/sekund). Ofte ses frekvensen angivet som en vinkelfrekvens med enheden radianer/sekund: w = 2 * Pi * f (her angiver Pi den matematiske værdi angivet med det græske bogstav Pi: 3.14159....)

Hele grundlaget for Fourier transformationen bygger på det faktum at mange signaler (og som oftest de signaler man arbejder med indenfor ingeniør- og signalbehandlingsområdet), kan nedbrydes i en uendelig række af sinusformet funktioner. Et eksempel vil synliggøre det.

Lad os antage at vi har følgende simple signal:



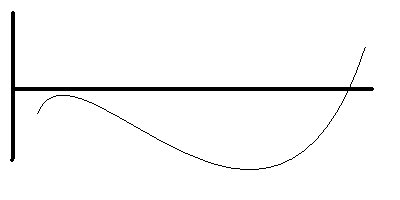
Et sådanne signal kan vi nedbryde i nogle sinusformet funktioner - så det kunne f.eks. se sådanne ud (dette er udelukkende et eksempel og skal kun ses som sådanne):



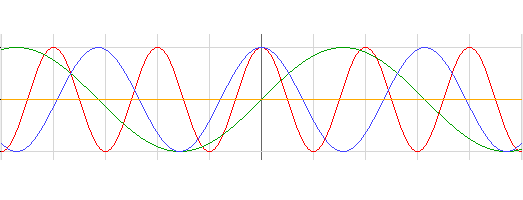
Ovenstående graf består udelukkende af sinusformet funktioner, og sådanne funktioner har alle en konstant frekvens. Med andre ord er det lykkedes os at få hænderne på vores signals frekvensinformation ved at nedbryde det oprindelige signal til nogle sinusformet funktioner. Sådan en række af sinusfunktioner kalder man en Fourier række og det gør os altså i stand til at udtrykke en funktion, f(t) som en uendelig række af sinusfunktioner:


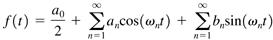
Vinkelfrekvensen, w_n, er givet ved udtrykket 2 * Pi * n * f. Koefficienterne a og b kan bruges til at udregne et signals energi ved en given frekvens f_n: E_n = (a_n)^2 +(b_n)^2. Denne brug af et signals Fourier-transformation til bestemmelse af dets energi ved forskellige frekvenser (et såkaldt enegispektrum) ses tit.

Ofte ses en Fourier række udtrykt på kompleks form, hvilket vil sige med [url=http://da.wikipedia.org/wiki/Komplekse_tal"]komplekse tal[/url]:



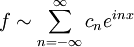
Hvor den komplekse udgave er mere kompakt, er det ikke så tydeligt længere hvad der egentlig foregår.

De komplekse koefficienter fra ovenstående udregnes som:



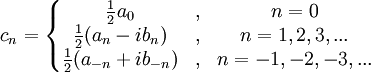
(ovenstående forudsætter man kender koefficienterne a_n)

Fourier transformationen bygger på den komplekse form af en Fourier række. Fouriertransformation af et kontinuert-tidssignal x(t) er givet ved:



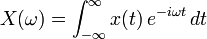
Hvis vi skal "den anden vej", dvs. fra frekvensdomænet til tidsdomænet, benytter vi den inverse Fourier transformation:



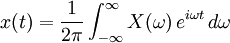
De Fourier transformationer som her er beskrevet er alle 1D og egner sig derfor til elektrisk signalbehandling. Der findes selvfølgelig også flerdimensionale Fourier transformationer som kan anvendes på f.eks. billeder. Vi vil dog i denne artikel udelukkende beskæftige os med 1D signaler som elektronik/akustik.

Den diskrete Fourier transformation i C#

Som vi så ovenfor er Fourier transformationen udtrykt ved et integral. Det er fint såvidt vi har et matematisk udtryk for vores signal. Det er dog sjældent tilfældet. I stedet har vi oftest, eller er i stand til at fremskaffe, nogle diskrete målinger at det pågældende signal (diskret i tid og frekvens). I disse tilfælde kan vi benytte den diskrete Fourier transformation som netop anvendes på sådanne diskrete målinger.

Hvis vi forestiller os at vi måler amplituden af vores signal N gange i løbet af tidsrummet T har vi N - 1 tidsintervaller, alle af samme længde. Hvis x_i angiver angiver den i'te måling har vi følgende målinger af vores signal x(t):

[x_0, x_1, x_2, . . ., x_N-2, x_N-1]

Forholdet mellem x_i og vores signal x(t) er da:



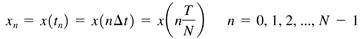
Samme fremgangsmåde kan vi bruge med signalet i frekvensdomænet. I stedet for at måle signalet i tidsdomænet i N lokationer adskilt af samme tidsinterval, tager vi nu målinger af signalet i frekvensdomænet i N lokationer adskilt af samme frekvensinterval, med en samplingfrekvens der hedder F = N/T. Så nu har vi følgende målinger af frekvensamplituden:

[X_0, X_1, X_2, . . ., X_N-2, X_N-1]

Ligesom med tidsdomænet ovenfor, kan vi nu opstille en formel for forholdet mellem målingerne og signalet i frekvensdomænet:



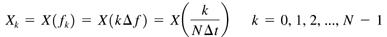
Hvis vi kombinerer dette med definitionerne for både forward og invers Fourier transformation ovenover, får vi følgende to definitioner for forward og invers diskret Fourier transformation.

Forward diskret Fourier transformation:



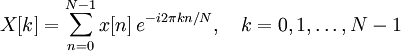
Invers diskret Fourier transformation:



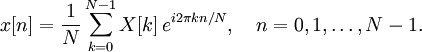
Vi har nu nok information til at kunne implementere en Fourier transformation i C#, men først skal vi dog lige havde udtrykt de to transformationer ved de trigonometriske funktioner (det gøres vha Eulers formel: = e^ix = cos(x) + i*sin(x)):

Forward transformation:



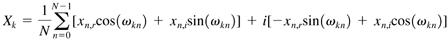
og den inverse:



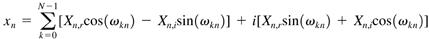
Som du måske har bemærket har vi i de to ovenstående formeler flyttet skaleringsfaktoren (1/N) til foward transformationen. Det har vi gjort for at kunne håndtere den situation hvor vores frekvens respons "eksploderer", hvilket kan være tilfældet på grund af summationen når vi har rigtig mange samplepunkter (og her betyder mange millioner). Der er intet problem i at flytte rundt på skaleringsfaktoren så længe produktet af de to skaleringsfaktorer giver 1/N; i dette tilfælde er faktoren på vores forward transformation lig med 1/N og på den inverse lig med 1, og produktet af de to tal giver jo netop 1/N.

En anden ting vi skal være opmærksom på er at selvom vores oprindelig data muligvis ikke indeholder komplekse tal, vil det transformerede data typisk indeholde data der har både en reel og imaginær komponent, det er derfor vigtigt at vi er i stand til at håndtere data der er komplekst. Det gør vi på følgende måde.

Vores funktion tager tre argumenter. Første argument er vores samples der skal transformeres. De indeholder både reelle og imaginære komponenter i par. Så f.eks. vil data[0] indeholde den reelle komponent af første sample, data[1] indeholder den imaginære komponent af første sample, data[2] indeholder den reelle komponent af anden sample osv. Såfremt vores samples ikke har en imaginær komponent sætter vi den blot til 0.0. På denne måde kan vi håndtere komplekse tal i vores samples. Andet argument er antallet af samples i vores data. Tredje argument er en boolsk værdi der er sand såfremt vi ønsker en forward transformation og falsk såfremt vi ønsker en invers transformation. Funktionen returnerer en liste af tal som er de transformerede samples. Denne liste indeholder båd den reelle og imaginære komponenter af de transformerede samples på samme måde som de oprindelige samples. På denne måde håndterer vi at resultatet af transformation kan være komplekse tal.

Koden for den diskrete Fourier transformation er:

namespace FourierTransform
{
    public class DiscreteFourierTransform
    {
        // dataToBeTransformed contains the data points to be transformed - both the real and imaginary components!
        // They are stored as pairs: the real first, followed by the imaginary. For example: dataToBetransformed[0] is the
        // real component of the first sample point, dataToBeTransformed[1] is the imaginary component of the first
        // sample point etc.
        public List<double> Transform(List<double> dataToBeTransformed, int numberOfSamplePoints, bool trueForForward)
        { 
            // Let's use N since we know that from the formulas
            int N = numberOfSamplePoints;

            //
            // Calculate the angle and handle the direction
            //            
            double omega = 2.0 * Math.PI / N;

            // If it is the inverse transformation we reverse the sign of the angle
            if(!trueForForward)
            {
                omega = -omega;
            }

            // Do the transformtion - we need to make space for both real and imaginary components of the data
            // points
            List<double> transformedPoints = new List<double>(2 * N);
            int indexOfRealComponent = 0;
            int indexOfImaginaryComponent = 0;
            for (int i = 0; i < N; ++i)
            {
                indexOfRealComponent = 2 * i;
                indexOfImaginaryComponent = 2 * i + 1;
                transformedPoints[indexOfRealComponent] = 0.0;
                transformedPoints[indexOfImaginaryComponent] = 0.0;
                for (int j = 0; j < N; ++j)
                {
                    transformedPoints[indexOfRealComponent] += dataToBeTransformed[2 * j] *
                        Math.Cos(omega * j * i) + dataToBeTransformed[2 * j + 1] *
                        Math.Sin(omega * j * i);
                    transformedPoints[indexOfImaginaryComponent] += -dataToBeTransformed[2 * j] *
                        Math.Sin(omega * j * i) + dataToBeTransformed[2 * j + 1] *
                        Math.Cos(omega * j * i);
                }
            }

            // We scale the forward transform with the 1/N factor. It doesn't matter whether we scale the
            // forward or inverse one, just as long as the product of the scaling factors equals 1/N
            if (trueForForward)
            {
                for (int i = 0; i < N; ++i)
                {
                    transformedPoints[2 * i] /= N;
                    transformedPoints[2 * i + 1] /= N;
                }
            }

            return transformedPoints;
        }
    }
}

Brug af Fourier transformationen

Lad os prøve vores Fourier transformation på en 2Hz cosinusfunktion: x(t) = cos(4*pi*t). Funktionen er afbilledet på følgende graf:



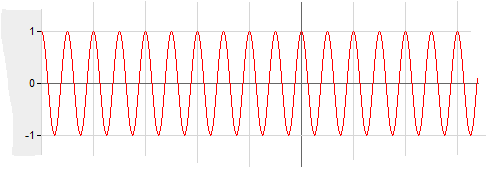
Vi vil tage 64 samples over en periode på 2 sekunder; 64 samples på 2 sek. selvfølgelig meget lidt, men det er fint nok til vores demonstrative formål.

I løbet af to sekunder har vi fire svingninger, så vi tager 16 samples per svingning.

Vores testprogram vil først sample cosinusfunktionen som nævnt, hvorefter vi bruger den diskrete Fourier transformation til at udregne frekvenspsektret.

Testkoden er som følger:

namespace FourierTransform
{
    class Program
    {
        static void Main(string[] args)
        {
            int N = 64;
            double[] samplePoints = new double[2 * N];

            // First we sample the 2 Hz sine wave            
            double T = 2.0;
            for (int i = 0; i < N; ++i)
            {
                samplePoints[2 * i] = Math.Cos(4.0 * Math.PI * i * T / N); // Reel component
                samplePoints[2 * i + 1] = 0.0; // We set the imaginary component to zero
            }

            // Now compute the DFT
            DiscreteFourierTransform dft = new DiscreteFourierTransform();
            double[] transformedPoints = dft.Transform(samplePoints, N, true);

            // Now we print out the frequency spectrum
            double fk = 0.0;
            for (int k = 0; k < N; ++k)
            {
                fk = k / T;
                Console.WriteLine("f["+k+"], freq. = " + fk + ": " +
                    transformedPoints[2*k] + " + " + 
                    transformedPoints[2*k + 1] + "i");
            }
        }
    }
}

Hvis du kører ovenstående program kan du se at der er en peak ved en frekvens på 2 Hz, hvilket er forventeligt. Underligt nok så er der også en peak ved 30 Hz. Det er fordi at ved vores 32 samples per sekund, udregner Fourier transformationen faktisk spektret for området -16 Hz til 16 Hz, vi skifter det blot så den negative del af spektret rykkes til 16 - 32 Hz området. Med andre ord er peaket ved 30 Hz faktisk et peak ved -2 Hz hvilket også er forventeligt .

FFT: Fast Fourier Transformation

En standard DFT som beskrevet og implementeret ovenfor er simpel og fungerer fint. Den har dog et problem. Antallet af operationer i en DFT er proportional med kvadratet på antallet af samplinger, det vil sige at ved store datamængder er den ganske ineffektiv. Derfor har man udviklet en hurtig Fourier transformation som utroligt nok hedder Fast Fourier Transform, eller FFT. Jeg vil ikke i denne artikel implementere FFT, blot gøre opmærksom på dens eksistens.

Afslutning

I denne artikel har vi kigget lidt på hvad en Fourier transformation er samt lavet en implementation af den i C#. Hvis du har fået blod på tanden og har lyst til at gå i dybden er Proakis bogen nævnt i begyndelsen værd af kigge nærmere i.

På gensyn...



Hvad synes du om denne artikel? Giv din mening til kende ved at stemme via pilene til venstre og/eller lægge en kommentar herunder.

Del også gerne artiklen med dine Facebook venner:  

Karma barometer (30 dage)

IT jobs | Kontakt | Om Udvikleren.dk | Om karma | IT nyheds arkiv | Annoncering

X