Tags:    java programmering

Indledning

I denne 12. del vil vi bevæge os ind i den del af Java Programmeringen, som er lidt mere avanceret. Dette betyder ikke at du nødvendigvis skal kunne alt hvad vi hidtil har lavet fuldstændig til punkt og prikke, men det betyder at du skal have styr på de allermest simple ting, såsom hvordan du laver objekter af klasser, hvordan du bruger variabler, og også hvordan du benytter array's i sin simpleste form. I denne artikel skal vi først og fremmest høre om rekursion. Vi skal se på hvad rekursion er, hvordan det virker, og selvfølgelig også se på fordele ved at benytte rekursion i ens java kode. Herefter vil jeg gennemgå nogle simple generiske kollektioner, og nogle har vi faktisk allerede haft fat i (ArrayList), og vi skal til allersidst lære at lave vores egen generiske kollektion. Så vi har nok spændende stof at tage fat på, så lad os komme i gang.

Rekursion

I programmering benytter man noget som kaldes for rekursion. Rekursion betyder at man har noget, som gentager sig selv. Hvad betyder dette så egentlig? Jo det betyder at hvis vi f.eks. har en metode, som inde i dens krop lavet et metode kald til sig selv, så er den rekursiv. Det vigtige når man benytter denne metode er at metoden har et stop punkt, akkurat ligesom med en løkke. Vi er nødt til at opsætte en betingelse for vores rekursive metode, ellers vil den bare kalde sig selv i uendelighed, hvilket til sidst vil lede computeren til et crash. Denne betingelse kalder vi for en sentinel, da den skal være vores vagt, som sikrer at vores rekursive metode ikke kalder sig selv for evigt.

Det bedste eksempel at bruge, når man skal vise hvordan rekursion virker, er ved at benytte det vi i matematik kalder for fakultet. Hvis vi f.eks. har 5! (! = fakultet), så kan vi benytte rekursion til at finde resultatet af dette.

 /**
  * Metode der kan beregne fakulteter af positive tal, ved hjælp af rekursion.
  * @return resultatet af beregningen, som en long værdi.
  */
 public long factorial(long n)
 {
    //returner 1, hvis nummeret er 1 eller mindre, ellers udfør rekursion.
    if (n <= 1) {
       return 1;
    }
    else {
       return n * factorial( n - 1 ); //kald denne metode endnu en gang (rekursion).
    }
 }

Hvis du indsætter tallet 5, som parameter i en System.out.println() statement, vil resultatet udskrive 120, da 5! = 120. Vi benytter som sagt rekursion, når vi skal beregne resultatet af 5!, og billedet nedenfor viser hvordan vores metode arbejder, når vi bruger rekursion.



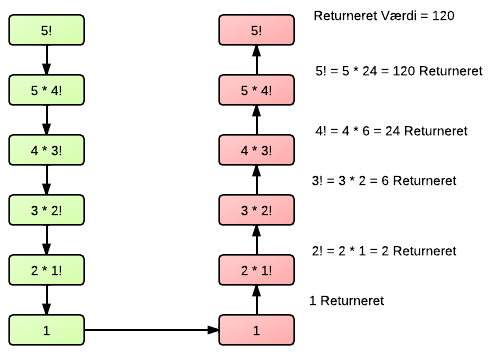
Vi kan se at vores metode starter ud med ikke at returnere noget, den kalder sådan set bare metoden igen, med nye værdier, indtil den når vores sentinel (vagt). Denne sentinel sørger for at stoppe metoden, og metoden stopper jo når vores værdi er 1 eller mindre end 1. Når den når sentinellen, begynder den på returnerings procedurende, det betyder at den begynder at returnerer de beregninger der blev lavet. Den returnerer værdierne til vores metode som kaldte den, og denne metode returnerer så også en ny værdi, baseret på dens udregning, indtil vi til sidst ender hos vores hoved metode kalder, som ofte er vores main metode. Det kan lyde lidt kryptisk, men er faktisk meget simpelt. Lad os tage den en gang til, den starter med at kalde sig selv, og lægger værdien på 'stakken' (computerens midlertidige memory), og det gør den indtil at den når vores sentinel. Vores sentinel sørger for at metoden ikke kaldes mere, og vi kan nu begynde at returnere de værdier, som vi i første omgang ønskede at returnere. Den går nu ind på 'stakken' (computerens midlertidige memory), og henter de værdier der blev gemt, og returnerer disse, indtil den når den sidste metode, hvor vores factorial( n ) metode blev kaldt fra (typisk main metoden).

Man kan sige at rekursion deler problemet op i mindre stykker, løser disse mindre problemer, for derefter at samle stumperne sammen igen. Dette princip kaldes også for 'Divide and Conquer Paradigm'. Dette er smart, da det ofte reducerer de linjer af kode, som man behøver at lave, og ofte er det også nemmere for programmøren at debugge og læse koden. Ulempen er dog at rekursive metoder kræver meget memory (specielt hvis de er store), da vi er nødt til at gemme ting på 'stakken', indtil at vi når vores sentinel. Vi fylder altså stakken op, og henter/fjerne først værdierne, når vores sentinel er nået. Dette er ofte også skyld i at performance bliver ringere, da det at kalde en metode kræver mere tid og plads, end at køre en almindelig løkke.

Så hvad skal du vælge? Du har sikkert opdaget at en rekursiv metode opfører sig lidt som en løkke, og ud fra hvad du lige har læst, så kan du ofte opnå bedre performance og i hvertfald mindre memory brug, ved hjælp af løkker. Jeg vil dog sige at du skal vælge at bruge rekursion, når performance ikke betyder helt så meget for dit program, men det kommer ofte meget an på hvad din metode laver og hvor mange gange den skal lave dette. Hvis performance derimod er et meget vigtigt element, og du ofte også har meget af gå igennem, så benyt dig af løkker i stedet. En sidebemærkning som du skal være opmærksom på, er at du kan altid konveretere en rekursiv metode, til at arbejde på en iterativ måde (med løkker), men at få en metode der arbejder iterativt (med løkker), til at arbejde rekursivt, kan ikke altid lade sig gøre.

Mini Opgave - Lav en rekursiv metode der udfører det som vi kender som potensopløftning. Metoden skal have 2 parametre, hvoraf den første er basen og den næste er eksponenten. Metoden skal gøre det at den skal returnere basen * med resultatet af vores recursive metodekald, indtil vores sentinel er nået. Sentinelen skal i dette tilfælde være så længe at eksponenten er mindre end eller lig med 1. Jeg kan hjælpe dig igang med at skrive metodens signatur - public int power(int base, int exponent) - Når du har løst opgaven, så sammenlign med min løsning. Bemærk at exponenten i dette eksempel kun må være et positivt tal (1 eller større).

 /**
  * Potensopløftning
  * @param base Basetallet, som skal opløftes.
  * @param exponent eksponenten, som basen opløftes i. skal være et positivt tal
  * @return resultatet af potensopløftningen som en int.
  */
 public int power(int base, int exponent)
 {
    //returner 0 hvis eksponenten er mindre end 1
    if (exponent < 1) {
       return 0;
    }
    //Vores sentinel for rekursionen
    else if (exponent == 1) {
       return base;
    }
    else {
       return base * power(base, exponent - 1); //kald metoden endnu en gang. (rekursivt kald)
    }
 }

Løsningen her benytter rekursion til at løse problemet med potensopløftning, og vi kan se at vores sentinel stopper metoden, når vores eksponent er 1. Vi kan også se at vores metode returnerer nul (og lave slet ingen rekursion), hvis eksponenten er nul eller negativ. Hvis ekspnenten er 1 returnerer vi her så bare basen, da basen * 1 = basen. Det er i vores else del at det sjove sker, denne køres nemlig hvis eksponenten ikke er negativ, eller lig med 1. Her returnerer vi basen * resultatet af vores metode, hvor eksponentent er reduceret med 1. grunden til at vi reducerer eksponenten med en, er for at den på et tidspunkt skal nå vores sentinel. Ellers vil metoden fungere lidt som en uendelig løkke. Bemærk også her at vi har delt problemet op, så den kalder sig selv, i stedet for at lave noget ekstra kompliceret. Ulempen ved denne måde at gøre det på, er at vi fylder op i stakken, og skal vi arbejde med store tal, kan performance godt blive nedsat, ved at bruge rekursion.

Mini Opgave - Tag nu opgaven fra før, men denne gang skal du lave metoden, hvor du ikke benytter rekursion. Du skal i stedet benytte dig af løkker. Metoden går nu fra at være rekursiv, til at være iterativ. Når du har løst denne opgave, så tag et kig på min løsning, og sammenlign. Bemærk at eksponenten kun må være et positivt tal (1 eller større)

 /**
  * Potensopløftning
  * @param base Basetallet, som skal opløftes.
  * @param exponent eksponenten, som basen opløftes i. Skal være et positivt tal (1 eller større)
  * @return resultatet af potensopløftningen som en int.
  */
 public int power(int base, int exponent)
 {
    //Returner 0, hvis eksponenten er mindre end 1
    if (exponent < 1) {
       return 0;
    }
    else {
       int result = 1;
 
       //multiplicer basen, med resultatet, indtil i er lig med eksponenten. 
       for (int i = 0; i < exponent; i++) {
          result *= base;
       }
 
       return result;
    }
 }

Her har vi metoden i en ikke rekursiv form, men en iterativ. Bedøm selv, men personligt syntes jeg at den rekursive er en lille smule lettere at læse og forstå, men mange gange er dette også en smagssag. Når vi har med rekursive metoder at gøre, kan vi nemt lave dem om til iterative metoder, men ikke altid omvendt. Kort opsummering, så er rekursion en måde at dele problemet op i mindre problemer, og på den måde løse problemet. Ulempen er dog at man fylder computerens stak (memory) hurtigere op, og ved store algoritmer/udregninger, kan dette betyde dårligere performance. Dette betyder dog ikke at du skal holde dig fra rekursion, da det i ngle tilfælde kan være med til at simplicificere et problem. Mange gange kan man f.eks. undgå en masse 'nested' if og else parenteser, ved at benytte rekursion. Til sidst vil jeg gerne lige henvise til endnu en måde at ansku rekursion på, med et eksempel der hedder 'Tower Of Hanoi'. Illustrationen nedenfor, viser tre stolper, hvor det handler om at få flyttet alle brikkerne fra den første stolpe til en af de to andre, ofte den tredje stolpe, uden at en større brik ligger oven på en mindre. Hver gang en brik fjernes, kan man sammenligne det med et rekursivt kald, og hver gang vi smider en brik fra den første stolpe til f.eks. den midterste, så lægger vi et resultat på stakken.



Et andet godt eksempel på tower of hanoi, er at finde her, hvor du kan lege med en lille java applet (java program på nettet), som viser netop dette med tower of hanoi.

Generiske Kollektioner

Nu springer vi lidt videre i teksten, og går fra at lære om rekursion, til at lære om nogle generiske kollektioner. Vi skal dog ikke bare høre om dem, men vi skal prøve at lave vores egen generiske kollektion. Når vi snakker om generiske kollektioner, snakker vi om kollektioner der kan indeholde alle slags typer af data. Vi kender en generisk kollektion allerede, og denne kollektion hedder ArrayList. Vi kan som vi ved gemme alle mulige slags typer af data i denne kollektion, bare ved at angive hvilken type af data vi ønsker at gemme. Der findes dog også andre typer af generiske kollektioner, som bl.a. hedder List, Map, Set, Stack og Queue. Disse kollektioner har hver deres fordele og ulemper, f.eks. kan kollektioner af typen Set ikke indeholde elementer der er ens. Hvis vi f.eks. har en Set kollektion der indeholder Integers, så kan denne kollektion ikke indeholde to af de samme tal. Lad os se på et hurtigt eksempel på hvordan vi kan bruge en Set kollektion, i dette tilfælde HashSet, som er en gren af Set.

 import java.util.Set;
 import java.util.HashSet;
 
 public class Test {
 
    /**
     * Example of using a Set collection. In this we use a HashSet.
     */
    public void hashSetCollectionExample()
    {
       //Opret et nyt HashSet. Husk at importere HashSet fra java.util pakken.
       Set<Integer> mySet = new HashSet<Integer>();
 
       //Initialiser det med tal, der ikke er ens!!
       for (int i = 0; i < 10; i++)
       {
          mySet.add( i );
       }
 
       //Udskriv hele vores sets indhold.
       System.out.println( "Our set contains: " + mySet );
    }
 
 } //End Of class Test

Som du måske kan se på koden benytter vi ikke nogen 'get' metode for at finde et specifikt element. Dette er fordi vores Set kollektion ikke er indekseret, som f.eks. en liste (f.eks. ArrayList). Du kan altså af denne grund ikke fjerne elementer fra listen via et indeksnummer. Måden du fjerner et element fra listen på, er ved at benytte metoden remove(Object obj), som kræver et objekt der skal være lig med det objekt, som den skal fjerne. Ønsker vi f.eks. at fjerne tallet 7, fra vores Set kollektion, skal vi altså skrive således

 mySet.remove( 7 );   //Fjerner tallet 7 fra vores kollektion

Koden vil her fjerne tallet 7 fra vores Set kollektion. Grunden til at vi ikke behøver indeks, er fordi vores Set kollektion ikke kan indeholde elementer, som er ens. Vores Set kollektion kan altså ikke indeholde to elementer med tallet 7, og derfor er det nu nemt for os at fjerne tallet 7. Bemærk selvfølgelig at det element man ønsker at fjerne selvfølgelig skal være tilstede i vores Set kollektion.

En anden kollektion vi har arbejdet meget med før i denne serie, er kollektionen ArrayList. ArrayList er en gren af list kollektionerne. Disse kollektioner der er underklasser fra klassen List, har den egenskab at de er ordnede med indeks, og de kan derfor også indeholde ens objekter. Der findes en kollektion kaldet en LinkedList, som også arver fra klassen List. En LinkedList har den egenskab at der efter hvert element, er en reference, til det næste element i listen. Det betyder at det første element, indeholder en reference, til det næste element o.lign. Man kalder også disse for noder, altså en node er et objekt, samt en reference, videre til den næste node, eller til null (ingen ting). En LinkedList har den fordel at man kan indsætte elementer og slette elementer midt i kollektionen, meget hurtigere, end i et ArrayList. Dog er et array list hurtigere, hvis du skal have data fra et bestemt sted i listen, da du nemmere kan komme til elementet. Det kan du fordi man ikke behøver at gå igennem hver node, for at få referencen til den næste node, indtil du når dit mål. En ArrayList gemmer nemlig elementerne direkte i hukommelsen, hvilket betyder at vi kan få adgang til et bestemt element betydeligt hurtigere med indeksering. En LinkedList gemmer ikke elementerne direkte på hukommelsen, men gemmer altså referencer til det næste element. Det kan derfor godt tage lidt længere tid at hente elementer i en LinkedList end et ArrayList. Herunder ser du en simpel illustration af en LinkedList. Som du kan se har hver node en reference til den næste node, og den sidste (også kaldet for lastnode), har en reference til null (ingen ting).



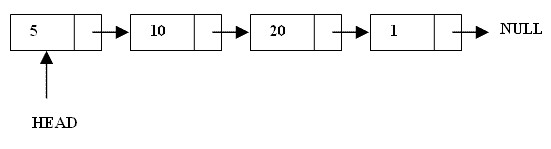
Lad os nu se på et eksempel på en LinkedList i java. Husk at du skal importerer klassen fra pakken java.util.

 import java.util.LinkedList;
 
 public class Test {
 
    //Eksempel på LinkedList
    public void linkedListExample()
    {
       //Opret LinkedList
       LinkedList<Integer> myLinkedList = new LinkedList<Integer>();
 
       //Indsæt elementer i vores linkedList, ved at kalde metoden add().
       for (int i = 0; i < 10;  i++)
       {
          myLinkedList.add( i );
       }
 
       //Udskriv nu elementerne i listen. Bemærk vi her benytter metoden get().
       for (int i = 0; i < myLinkedList.size(); i++)
       {
          System.out.print( myLinkedList.get( i ) + " " );
       }
    }
 
 }

Faktisk er LinkedList og ArrayList ret ens, og det er de bl.a. fordi de begge benytter List som deres superklasse. Performance mæssigt er der de forskelle der blev specificeret før, men for almindelige applikationer der det ikke den helt store forskel der der er i ydelsen, når vi skal finde elementer. Kig evt. selv på dokumentationen af LinkedList og ArrayList i java biblioteket, for at lære mere om disse kollektioner.

Herefter findes der en kollektionstype som hedder en Map. Et Map er kendetegnet ved at vi har både en nøgle of en dertil hørende værdi. Nøglen skal bruges for at finde værdien. Man kan sige at et indeks fungerer lidt ligesom en nogle for den værdi den er indeks for, men i et Map kan nøglen være meget andet end bare et indeksnummer. Vi kan f.eks. have nøgler, som er strenge i stedet for integers. Der findes forskellige Maps, men den mest brugte er den som hedder et HashMap. Et HashMap er altså en kollektion der har en nøgle og en værdi tilknyttet denne nøgle. Nøglen skal derfor altid være unik, medens værdi ikke behøver at være unik. Hvis vi f.eks. har et Map hvor både nøglen, men også værdierne er unikke, kalder man det for en en-til-en mapping, medens hvis kun nøglen er unik, kaldes det for en mange-til-en mapping. Lad os se på et eksempel, hvor vi benytter et HashMap (findes i pakken java.util).

 import java.util.HashMap;
 
 public class Test {
 
    public void hashMapExample()
    {
       //Opret HashMap. Bemærk at vi skal både definere datatype for nøglen og værdien.
       HashMap<String, Integer> myHashMap = new HashMap<String, Integer>();
 
       //Indsæt elementer i vores HashMap
       myHashMap.put("food", 1);
       myHashMap.put("drink", 2);
       myHashMap.put("candy", 3);
       myHashMap.put("nothing", 4);
 
       //Udskriv vores elementer med metoden get( key ).
       System.out.println( myHashMap.get("food") );
       System.out.println( myHashMap.get("drink") );
       System.out.println( myHashMap.get("candy") );
       System.out.println( myHashMap.get("nothing") );
    }
 
 }

Som du kan se får vi fat i vores elementer ved hjælp af den specificerede nøgle. Vi kunne også benytte andet en strenge som nøgle. Ja selv dine egne objekter kan være en nøgle, du skal bare huske at specificerer dette som datatypen. Du skal dog altid huske på at nøglen altid skal være unik.

Til sidst skal vi kigge på henholdsvis kollektionerne Stack og Queue. Hvis vi starter med Stack, så går den efter princippet der hedder First In Last Out (FILO), hvilket betyder at det første element der kommer ind i vores stack, også altid er det element der kommer sidst ud igen. Tænk på som at du står og vasker tallerkner op. Hver gang du har vasket en tallerken putter du denne tallerken på stakken af tallerkner ved siden af dig. Når du har vasket tallerknerne, og skal til at tørre dem, tager du selvfølgelig den tallerken der ligger øverst, men dette var jo også den tallerken du sidst vaskede, altså FILO princippet. Se evt. illustrationen nedenunder.



push() og pop() er henholdsvis også de termer man bruger, når man henholdsvis pusher elementer på stakken, mens man popper elementer fra stakken igen. Lad os se på eksempel på hvordan du kan bruge en stack.

 import java.util.Stack;
 
 public class Test {
 
    public void stackExample()
    {
       //Opret stack
       Stack<Integer> myStack = new Stack<Integer>();
 
       //push elementer til stakken.
       for (int i = 0; i < 5; i++)
       {
          myStack.push( i );
          System.out.println( "Pushed: " + i );
          System.out.println( "Stack contains: " + myStack + " (top)" );
       }
 
       System.out.println();
 
       //Pop elementer fra stakken
       while ( !myStack.isEmpty() )
       {
          int poppedElement = myStack.pop();
          System.out.println( "Popped: " + poppedElement );
          System.out.println( "Stack Contains: " + myStack + " (top)" );
       }
    }
 
 }

Hvis du nu f.eks. kører metoden, vil du få et output der ligner nedenstående billede



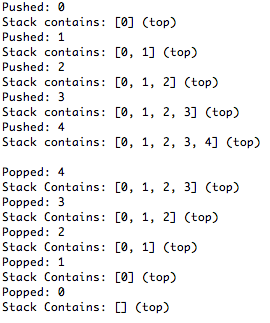
Som du kan se popper den det sidste element i vores stack, altså ligesom når vi tog opvasken med tallerknerne. En Queue derimod virker ligesom en 'kø' i det lokale supermarked. Den går nemlig efter princippet First In First Out (FIFO), altså at den sam kommer forrest i køen er også den der kommer først til. Vi kender det fra det lokale supermarked, men også bare hvis vi ringer op til vores telefonselskab. Der bliver vi ofte fortalt hvilket nummer vi har i køen. En queue er dog ikke en almindelig klasse, men et interface, og vi skal derfor benytte nogle af dens underklasser for at benytte en queue. En LinkedList implementerer bl.a. Queue interfacet, og vi kan derfor få en LinkedList til at opføre sig som en Queue. Metoderne man bruger her er metoden offer(), for at at indsætte elementer til køen, samt enten peek() eller poll(), for at trække elementer ud af listen igen. Forskellen på peek() og poll(), er at peek() kun henter elementet ud af køen, den sletter den ikke, medens poll(), henter elementet ud af køen og sletter det herefter fra køen. Lad os se på et eksempel på en Queue.

 import java.util.LinkedList;
 import java.util.Queue;
 
 public class Test {
 
    public void queueExample()
    {
       //Opret Queue, ud af en LinkedList
       Queue<Integer> myQueue = new LinkedList<Integer>();
 
       //Offer elementer til vores queue.
       for (int i = 1; i <= 5; i++)
       {
          myQueue.offer( i );
          System.out.println( i + " offered to the queue" );
       }
 
       System.out.println();
 
       while ( !myQueue.isEmpty() )
       {
          System.out.println( myQueue.poll() + " is polled from the queue" );
       }
    }
 
 }

Hvis du nu kører metoden, vil du få et resultat som billedet nedenfor.



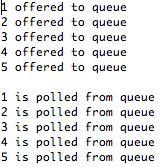
Det vigtige ved at kende disse generiske kollektioner, er at det er vigtigt at vælge den rigtige kollektion til det rigtige formål. Har du brug for en liste der ofte skal have indsat elementer i midten af kollektionen, frem for i slutningen, så er en LinkedList oftere en bedre løsning end en ArrayList. Skal du bare have overført dine unikke elementer til en kollektion, kan du med fordel benytte en Set kollektion. Skal du dog bare have gemt dine elementer, men ordnen de kommer ind i er ikke ligegyldig, så kan en stack, eller en queue måske være den bedste løsning. Hvis ingen af disse fungerer som vi ønsker det, så kan vi også sætte os ned og lave vores egen generiske kollektion.

Vores egen generiske kollektion

Kun fantasien sætter grænser her, men for at gøre det simpelt, så lad os tage en af de simple og i mine øjne lidt sjove kollektioner, som vi allerede har hørt lidt om. Stack kollektionen, der fungerede med princippet FILO, kan vi nu lave en efterligning af, som samtidig er generisk. Generisk betød at det var en klasse/kollektion, der kunne bruge alle mulige slags typer af data, så længe at vi huskede at specificere hvilken type det var der skulle bruges. Men før at vi laver den generisk, så lad os arbejde med integers, så vi nemmere kan få bygget selve vores stack op. Stacken havde to meget brugte metoder, nemlig push og pop. Push for at lægge på stakken, og pop, for at tage af stakken igen. Vi vil også få brug for en metode der kan tjekke om vores stack er tom, så vores stack klasse, skal altså have tre metoder - push(), pop() og isEmpty() - Skelettet ser nu således ud

 /**
  * MyStack is our own stack collection class. It works like
  * a normal stack, with the principle of FILO (First In Last Out).
  * Version 1.0 only works with integers, so at the moment
  * our stack is not a generic collection.
  * 
  * @author Martin Rohwedder
  * @version 1.0 (27-1-2012)
  */
 public class MyStack {
 
     /**
      * Constructor of MyStack objects
      */
     public MyStack()
     {
         
     }
     
     /**
      * Push an element on to the stack
      * @param element The element to be pushed.
      */
     public void push(int element)
     {
         
     }
     
     /**
      * Pop the top element from the stack.
      * @return the top element of the stack.
      */
     public int pop()
     {
         return -1;
     }
     
     /**
      * Check if our stack is empty
      * @return true if the stack is empty
      */
     public boolean isEmpty()
     {
         return true;
     }
     
 }

Nu kan vi begynde at lave vores stack. Du er velkommen til selv at lave koden og herefter kigge på min løsning, da jeg vil påstå at det lærer du mest af. Jeg kan dog give lidt hjælp, at jeg i min løsning vil bruge en arraylist, til at indeholde de elementer, som kommer ind i vores stack. Når du har 'løst' opgaven, kan du sammenligne med min, og hvem ved, måske er din løsning bedre!

 import java.util.ArrayList;
 
 /**
  * MyStack is our own stack collection class. It works like
  * a normal stack, with the principle of FILO (First In Last Out).
  * Version 1.0 only works with integers, so at the moment
  * our stack is not a generic collection.
  * 
  * @author Martin Rohwedder
  * @version 1.0 (27-1-2012)
  */
 public class MyStack {
     
     //Object Variables
     private ArrayList<Integer> buffer;   //Buffer which should contain our elements
 
     /**
      * Constructor of MyStack objects
      */
     public MyStack()
     {
         buffer = new ArrayList<Integer>();
     }
     
     /**
      * Push an element on to the stack
      * @param element The element to be pushed.
      */
     public void push(int element)
     {
         buffer.add(element);
     }
     
     /**
      * Pop the top element from the stack.
      * @return the top element of the stack.
      */
     public int pop() throws IndexOutOfBoundsException
     {
         if (!isEmpty())
         {
             int element = buffer.get( buffer.size() - 1 );
             buffer.remove( buffer.size() - 1 );
             return element;
         }
         else
         {
             throw new IndexOutOfBoundsException("MyStack is empty!");
         }
     }
     
     /**
      * Check if our stack is empty
      * @return true if the stack is empty
      */
     public boolean isEmpty()
     {
         return buffer.isEmpty();
     }
     
 }

Således kunne en løsning se ud. Stack er en meget simpel kollektion at lave, og dette er også grunden til at jeg har valgt netop denne kollektion, da vi nødig skulle begynde at rode os ud i for meget hurlumhej, når vi skal til det vigtige i dette afsnit. Det vigtige, spørger du måske om, hvad kan det være? Jo det vigtige er at lære noget om hvordan vi laver generiske kollektioner. Lige nu har vi lavet en stack kollektion, men den er ikke generisk overhovedet. Den kan nemlig kun indeholde integer datatyper, hvilket ofte ikke er det eneste man ønsker at gemme i en stack. Man kunne nu lave f.eks. en klasse for hver af de primitive datatyper vi kender, men dette er en meget ustabil og kluntet løsning. Hvad nu hvis vi ikke ønsker at bruge primitive datatyper, men gerne vil gemme objekter af vores egen konstruerede klasse f.eks. Så kan vi pludselig ikke bruge den kollektion. En anden løsning kunne være at lade vores kollektion kunne tage datatypen Object. Object er jo superklassen over alle superklasser. Alle klasser, også dem du selv laver, arver automatisk fra denne klasse. Straks har vi fundet en måde at løse problemet på, men nu opstår der så et nyt problem. Fordi når du returnerer objekter af typen Object, er du nødt til at caste objekterne hver eneste gang, da de ellers vil opføre sig som Object objekter (Casting betyder at man fortæller at en superklasse skal agere som en underklasse), og ikke f.eks. Integer objekter. Dette gør brugen meget kluntet, og det er hyppigere at der kan ske fejl, hvis man f.eks. glemmer at caste rigtigt. Der findes dog også en langt nemmere og mere fejlfri metode, som man kan gøre brug af, for at opnå den generiske effekt.

Metoden går ud på at man med nogle simple syntaksbegreber, kan fortælle java at denne datatype er generisk, altså den kan være alt muligt, indtil vi skal bruge den, så er vi nemlig nødt til at specificere datatypen. Måden man gør dette på, er ved at skrive < T > i ens klassedeklaration, lige efter klassens navn. symbolerne < og > betyder at vi her ønsker en generisk datatype. Klassen skal altså arbejde med en generisk datatype, hvilket betyder at vi hver gang vi skal oprette objekter af klassen er nødt til at fortælle java hvilken datatypen klassen skal kunne arbejde med. På denne måde kan sikre at vi kan bruge alle mulige datatyper. Bogstavet T er bare det officielle bogstav, når man laver sine egne generiske klasser, men vi kunne også have skrevet G, bare du benytter det samme igennem hele klassen. Vores klasse ser nu således ud

 import java.util.ArrayList;
 
 /**
  * MyStack is our own stack collection class. It works like
  * a normal stack, with the principle of FILO (First In Last Out).
  * Version 2.0 works with generic types
  * 
  * @author Martin Rohwedder
  * @version 2.0 (27-1-2012)
  */
 public class MyStack < T > {
     
     //Object Variables
     private ArrayList<Integer> buffer;   //Buffer which should contain our elements
 
     /**
      * Constructor of MyStack objects
      */
     public MyStack()
     {
         buffer = new ArrayList<Integer>();
     }
     
     /**
      * Push an element on to the stack
      * @param element The element to be pushed.
      */
     public void push(int element)
     {
         buffer.add(element);
     }
     
     /**
      * Pop the top element from the stack.
      * @return the top element of the stack.
      */
     public int pop() throws IndexOutOfBoundsException
     {
         if (!isEmpty())
         {
             int element = buffer.get( buffer.size() - 1 );
             buffer.remove( buffer.size() - 1 );
             return element;
         }
         else
         {
             throw new IndexOutOfBoundsException("MyStack is empty!");
         }
     }
     
     /**
      * Check if our stack is empty
      * @return true if the stack is empty
      */
     public boolean isEmpty()
     {
         return buffer.isEmpty();
     }
     
 }

Indtil videre gør den ikke noget særligt, da vi kun har fortalt java at klassen kan modtage en generisk type. Vi er også nødt til at bruge den inde i selve klassen. F.eks. skal vores ArrayList nu ikke indeholde Integers, men den skal indeholde vores generiske type T. Metoden pop() skal heller ikke returnerer en int, men vores generiske datatype T. Og metoden push() skal selvfølgelig heller ikke have en integer som parameter, men et element der har vores T som datatype Vores klasse ser nu således ud

 import java.util.ArrayList;
 
 /**
  * MyStack is our own stack collection class. It works like
  * a normal stack, with the principle of FILO (First In Last Out).
  * Version 2.0 works with generic types
  * 
  * @author Martin Rohwedder
  * @version 2.0 (27-1-2012)
  */
 public class MyStack < T > {
     
     //Object Variables
     private ArrayList< T > buffer;   //Buffer which should contain our elements
 
     /**
      * Constructor of MyStack objects
      */
     public MyStack()
     {
         buffer = new ArrayList< T >();
     }
     
     /**
      * Push an element on to the stack
      * @param element The element to be pushed.
      */
     public void push(T element)
     {
         buffer.add(element);
     }
     
     /**
      * Pop the top element from the stack.
      * @return the top element of the stack.
      */
     public T pop() throws IndexOutOfBoundsException
     {
         if (!isEmpty())
         {
             T element = buffer.get( buffer.size() - 1 );
             buffer.remove( buffer.size() - 1 );
             return element;
         }
         else
         {
             throw new IndexOutOfBoundsException("MyStack is empty!");
         }
     }
     
     /**
      * Check if our stack is empty
      * @return true if the stack is empty
      */
     public boolean isEmpty()
     {
         return buffer.isEmpty();
     }
     
 }

Nu kan du jo teste din nye kollektion, og prøve at bruge flere datatyper. Vi kan altså oprette objekter af kollektionen, og herved definere den datatype den skal indeholde, ligesom når vi bruger en almindelig arraylist, eller en anden kollektion. Vores main kunne nu se således ud til test af kollektionen!

 public static void main(String[] args)
 {
     //Create object of our stack collection
     MyStack<String> stack = new MyStack<String>();
     
     try
     {
         //Push elements to stack
         System.out.println("Pushed: Burger");
         stack.push("Burger");
         System.out.println("Pushed: Spaghetti");
         stack.push("Spaghetti");
         System.out.println("Pushed: Ham");
         stack.push("Ham");
         
         System.out.println();   //empty line!
     
         //Pop elements from stack!
         System.out.println("Popped: " + stack.pop());
         System.out.println("Popped: " + stack.pop());
         System.out.println("Popped: " + stack.pop());
         
         //Pop one element more than the stack contains
         System.out.println("Popped: " + stack.pop());
     }
     catch (IndexOutOfBoundsException ex)
     {
         System.out.println("\nException: " + ex.getMessage());
     }
 }

Denne test, tester med strenge, men du kan også prøve at lave test hvor den indeholder integers, doubles osv. ja selv objekter af dine egne domæne klasser.

Yderligere teori om 'hjemmelavede' generiske typer

Der er lige en ekstra ting som du skal vide, når du laver klasser og metoder der benytter en generisk type. Den ting er at du kan lade typerne arve fra andre klasser, som du så kan bruge i selve metoden eller klassen. Vi kan f.eks. tage dette eksempel

 public static <T extends Comparable<T>> T maximum(T x, T y, T z)
 {
     T max = x;   //Sæt x som maximum fra start
     
     //tjek om y er større end maximum variablen
     if (y.compareTo( max ) > 0)
     {
         max = y;
     }
     
     //Tjek om z er større end maximum variablen
     if (z.compareTo( max ) > 0)
     {
         max = z;
     }
     
     return max;
 }

Metoden her kan du bruge til at finde den største imellem tre typer. Hvis vi indsatte integers, ville den finde den største integer, og hvis vi indsætte strenge, vill den finde den længste streng. Det specielle ved denne metode er at vi for denne metode alene kan benytte os af Comparable klassens muligheder, da metoden specifikt nedarver fra denne klasse. Lad os tage et kig på signaturen - public static <T extends Comparable<T>> T maximum(T x, T y, T z) - Public static er henholdsvis metodens scope/adgang og specifikation af at metoden er tilgængelig uden at bruge et objekt af klassen. Dette er immervæk noget vi gerne skulle vide, så det springer vi let henover. Det vigtige er sådan set dette - <T extends Comparable<T>> - Dette fortæller java at vores metode benytter sig af en generisk datatype. Denne datatype vil altid arve fra klassen Comparable, da vi har specificeret dette ved at skrive extends Comparable<T>. Som du kan se er Comparable klassen også en generisk klasse, der kan tage generiske typer. Vi ønsker at benytte vores generiske type i denne Comparable klasse, og derfor har den <T> tilføjet. Simpelt nok fortæller dette bare java at vores metodes generiske type altid arver fra Comparable klassen. Vores metode har en returtype der hedder T, det betyder at metoden returnerer et objekt med vores generiske datatype. Vi kunne også have skrevet - public static <T extends Comparable<T>> void maximum(T x, T y, T z) - Her har vi skrevet void i stedet for T til sidst, hvilket jo gør at metoden bliver til en mutator og derfor ikke returnerer noget. Hvis vi skulle skrive metoden op med fagtermer, kunne vi skrive således - Adgang "klassemetode (valgfrit)" < Generisk-Datatype extends Klassenavn > Returtype metodenavn( parametre ) - Pointen med det hele er at det er vores metodes generiske type der arver fra Comparable klassen i vores eksempel. Det betyder at vi kun kan bruge Comparable inde i denne metode, og ikke udenfor metoden. Desuden er det faktisk ikke metoden som arver fra Comparable klassen, men vores generiske datatype. Så hvis vi satte integers ind som parametre i metoden ville det være integers der arvede fra denne Comparable klasse. Dette er dog lidt henne i det mere avancerede hjørne og er i mine øjne ikke så meget brugt. Dette er dog ikke ensbetydende med at det ikke er vigtigt at vide noget om, da du kan støde på det en gang i mellem.

Dette var hvad jeg havde tænkt mig at gennemgå i denne artikel. Vi har her kigget på rekursion, hvordan dette fungerer, og hvad det er. Vi har hørt og lært om nogle andre kollektioner der er brugbare at kende til i Java. Der findes dog flere end dem jeg har gennemgået, og du kan altid finde flere, ved at kigge i java biblioteket/API'et. Vi har til sidst lært at lave vores egne generiske klasser og metoder. Vi har lavet et simpelt eksempel på en generisk kollektionsklasse der benytter teknikkerne vi kender fra Stack kollektionen. Formålet med at lave noget generisk, er at det kan tilpasses alt. Det er immervæk smart at have en kollektion som vi bare kan specificerer hvilken datatype den skal indeholde, også kan det indeholde dette, fremfor en kollektion der er lavet specifikt til en bestemt datatype.

Hvad synes du om denne artikel? Giv din mening til kende ved at stemme via pilene til venstre og/eller lægge en kommentar herunder.

Del også gerne artiklen med dine Facebook venner:  

Karma barometer (30 dage)

IT jobs | Kontakt | Om Udvikleren.dk | Om karma | IT nyheds arkiv | Annoncering

X